Teaching Math
with Puzzle Games
Domain:
Subject:
Format:
Delivery:
Mathematics
Group Theory
Video Game
Puzzles
About This Project
I built a video game with puzzle systems that directly implement the axioms of group theory, a branch of abstract algebra.
Players reason about finite groups by interacting with them and building knowledge to solve challenges.
Contents
​
​​​​​​​
​
Teaching Principles as Design Values
​​
Agency as Essential to Learning
​​​​​​​
Teaching Moments
Example #1: "The Rotating Gates Hallway"
The Setup
The player must go through the hallway by aligning three gates.
The Key Player Insight
As long as the gates keep rotating concurrently, no path through will emerge.
The player must target a single gate first while planning ahead.
The Math Idea the Interaction Expresses
When two or more cycling objects move together at a fixed rate, whether or not all possible configurations are hit depends on relatively prime numbers.
​
Configurations will be missed when there are common factors in the number of turns it takes for cycling objects to return to their start positions.
Try it out ⤴︎
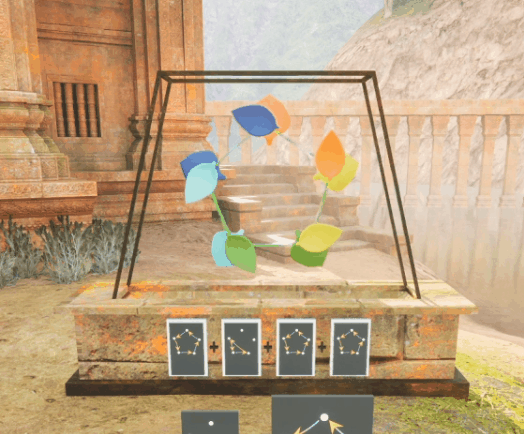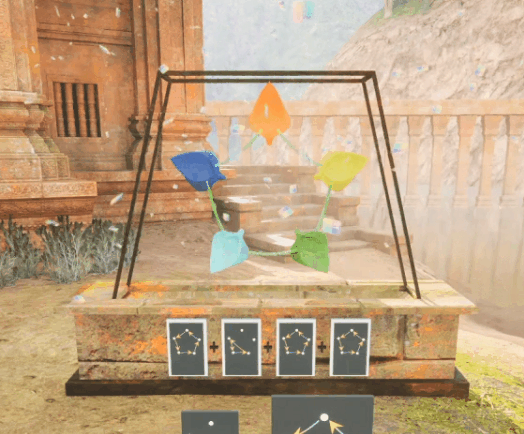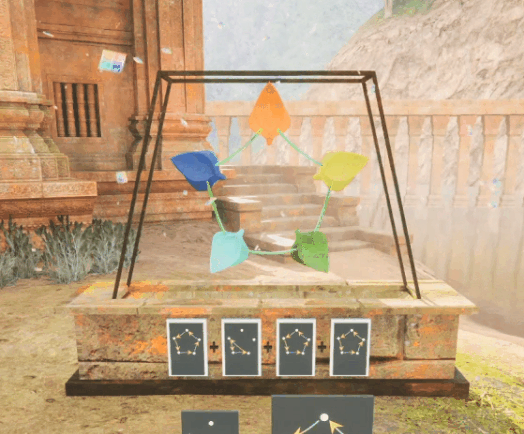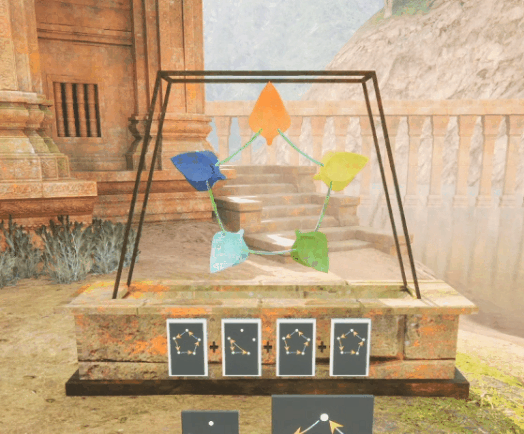
Example #2: "Puzzle Sequence for Partial Commutativity"
The Setup
The player must get each petal onto its matching leaf using a handful of cards.
The Key Player Insight
Order makes a difference in the resulting puzzle state for some pairs of cards and not others.
The Math Idea the Interaction Expresses
Commutativity (the ability to reorder freely) can exist between pairs of group elements,
without holding as a global property of that group.
Teaching Principles as Design Values
Teaching Principle (Design Value) #1: Agency is Essential to Learning
Learning Happens Through Action
Learning is participatory. Getting it right is rewarded.
Four-Step Puzzle Design
-
The player sees the goal.​
-
Next, they see the available objects and interactions.
-
The player works out a solution in their mind.
-
Lastly, they carry out the steps to solve it.
When steps are skipped or happen out of order, puzzles stop producing insight for the player and become a different kind of work.
​
Puzzles must be presented deliberately so that players notice the goal and supporting interactions immediately, think through a solution, and check their understanding by trying it out.
Teaching Principle (Design Value) #2: Transferrence by Design
Same Math Object, Many Interfaces
Finite groups from abstract algebra are presented repeatedly in many forms.
Transferrence at Play
When the player recognizes the same structure through a variety of surface forms, every insight applies again later, empowering them to solve puzzles with prior knowledge.
Teaching Principle (Design Value) #3: Sequencing Strategies
Environment Puzzles: A Part-Whole Approach
Rules and interactions are learned in isolation.
The entire environment puzzle is solved in sections.
This approach orients the learner just-in-time toward different surface forms
of the same math structure.
Puzzle Machines: A Whole-Part Approach
The player focuses on the whole until an individual puzzle is solved.
Concepts are expressed within a puzzle and repeated across puzzles.
This approach enables quick repetition and mastery of targeted math concepts.
End Note
I am always happy to talk through my design process further in person.
Thank you for reading!